I/ Définition
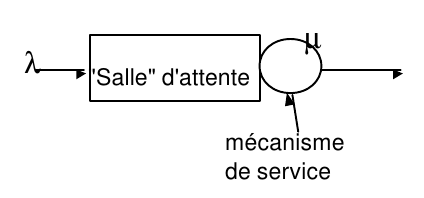
Une file d’attente est caractérisée par :
– Un flot d’arrivées
– Un mécanisme de service
– Une file d’attente
– Une discipline de service
Capacité de la file d’attente:
– nombre de places possibles : limité ou illimité.
– Si capacité limitée: les clients supplémentaires sont perdus ou rejoignent une autre file d’attente.
– Le nombre de clients dans le système est différent du nombre de clients dans la file d’attente
Discipline de service:
- règle d’ordonnancement des clients au service.
- FIFO: first in first out (exemple file d’attente à la sécu, 1er arrivé 1er servie)
- LIFO : Last in first out (ex: l’ascenseur: dernier rentré, premier sortie)
- PS : processor sharing, un serveur donne à chaque client en attente une “tranche” de service. (c’est du partage de ressources, le processeur accomplit un bout de tache sur un client puis passe au suivant … )
- ALEA un serveur libre choisit un client au hasard dans la file
- Priorité: on ajoute une suite Un, n appartient à N+, au flot des arrivées où Un est une variable aléatoire prenant ses valeurs dans l’ensemble des classes de priorités P. Un=i, signifie que le neme client, arrivant au temps Tn est de la classe i.
- Priorité préemptive : le programme preemptif passe en premier devant tous les autres et est servi en premier
Notation de KENDALL A/B/C/D/E
– A: statistique du processus d’arrivée (M = markovien; D=déterministe; G=générale)
– B: statistique des lois de service (M = markovien; D=déterministe; G=générale)
– C: nombre de serveurs
– D: nombre de clients dans le système
– E: discipline du service
– M/M/1 ==> Modèle le plus classique
– M/M/5/20
– M///5/infini/LIFO
LOI DE LITTLE
cette loi part du principe que sur le terme, la vitesse d’arrivée = vitesse de traitement
HYPOTHESES
- Lorsqu’un client, ayant terminé son service, quitte le système, il laisse, en moyenne, derrière lui, un nombre de clients égal à E(k). Ce client a trouvé en arrivant E(k) clients déjà présents et a passé dans le système un temps, E(T).
- Nous supposons que:
- Le nombre moyen des arrivées est égal au nombre moyen des départs du système.
- La longueur moyenne de la file lors des arrivées est égale à la longueur moyenne de la file lors des départs
ENONCE
- Si on appelle, l, le taux moyen des arrivées on a:
Nombre moyen de clients arrivés pendant le séjour du client dans le système = $\lambda$ E(t) = nombre moyen de clients qu’il laisse
Et en régime permanent, si T temps passé dans la file :
$\bar N$ : nombre de client dans le système
$\lambda$ : taux moyen d’arrivé des clients
$\bar T$ : temps passé dans la file
VALIDITE
– Régime permanent
– Les formules de Little sont valides pour les files G/G/S. Elles ont un caractère très général. En effet, il n’ y a aucune restriction quant à :
la loi d’arrivée, la loi des services, le nombre de serveurs.
– Elles peuvent prendre en compte le cas où il existe plusieurs classes de clients mais la discipline de service doit être définie, nous avons considéré la discipline FIFO.
II/ File M/M/1
M/M/1 = statistique du processus d’arrivée : markovien / statistique des lois de service : markovien / 1 serveur
Les formules à retenir:
État: nombre de clients, k, dans le système
Taux de trafic, r (charge, activité du serveur):
- Condition de stabilité:
- activité du serveur <1
- $\lambda<\mu$
- Débit d’entrée < débit du serveur
- Temps moyen inter-arrivée > temps de service moyen
- Si serveur saturé ($\rho$–>1):
- La distribution des intervalles de temps séparant deux départ consécutifs de la file saturée tend vers la distribution des temps de service
Nombre moyen de clients dans le système, N
Nombre moyen de clients dans la file, E(v)
$E(\nu) = \rho^2 \over 1-\rho$
$\rho$ : Taux de traffic
$E(\nu)$ : Nombre moyen de client dans la file
Temps moyen, T, passé par un client dans le système
$\bar T = 1 \over \mu1 \over 1-\rho$
$\rho$ : taux de traffic
$\bar T$ : temps passé par un client dans le système
$\mu$ : taux moyen de traitement, débit du serveur, taux de service
III/ File M/M/S
M/M/S = statistique du processus d’arrivée : markovien / statistique des lois de service : markovien / S serveurs
Les formules à retenir:
Taux de trafic
Nombre moyen de guichets, g, occupés:
$\bar g = \lambda \over \mu$
$\bar g$ : Nombre de guichets occupés
$\lambda$ : taux moyen d’arrivée des clients
$\mu$ : taux moyen de traitement, débit du serveur, taux de service du serveur
Nombre moyen de clients, v , dans la file:
k>s, k: nombre de clients, s nombre de serveurs
$\nu= 1 \over S!S \left (\lambda \over \mu \right) ^S+1 1 \over \left(1- \lambda \over S \mu\right)^2 \rho_0$
$\nu$ : nombre moyen de clients dans la file
$\lambda$ : taux moyen d’arrivée des clients
$\mu$ : taux moyen de traitement, débit du serveur, taux de service du serveur
$\rho_0$ : probabilité qu’il y ait 0 client dans le système
S : nombre de serveurs
Temps d’attente moyen, tf , dans la file:
$t_f= 1 \over S! \left(\lambda \over \mu \right)^S 1 \over S\mu 1 \over \left (1- \lambda \over S\mu \right )^2\rho_0$
$t_f$ : temps d’attente moyen des clients dans la file
$\lambda$ : taux moyen d’arrivée des clients
$\mu$ : taux moyen de traitement, débit du serveur, taux de service du serveur
$\rho_0$ : probabilité qu’il y ait 0 client dans le système
S : nombre de serveurs
Nombre moyen de clients dans le système
$\bar N= \lambda \over \mu \left ( \mu \bar t _f +1 \right)$
$\bar N$ : Nombre de client dans le système
$t_f$ : temps d’attente moyen des clients dans la file
$\lambda$ : taux moyen d’arrivée des clients
$\mu$ : taux moyen de traitement
Temps d’attentes dans le système
$\bar T= \bar N \over \lambda$
$\bar T$ : temps d’attente dans le système
$\bar N$ : Nombre de client dans le système
$\lambda$ : taux moyen d’arrivée des clients