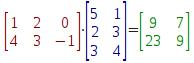Catégorie : RCP101 : Recherche opérationnelle et aide à la décision
-
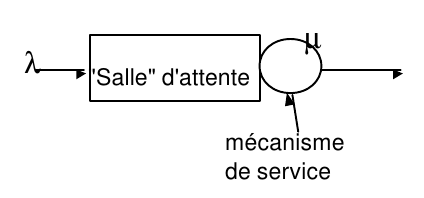
Les files d’attentes
I/ Définition Une file d’attente est caractérisée par : – Un flot d’arrivées – Un mécanisme de service – Une file d’attente – Une discipline de service Capacité de la file d’attente: – nombre de places possibles : limité ou illimité. – Si capacité limitée: les clients supplémentaires sont perdus ou rejoignent une autre file…
Écrit par
-
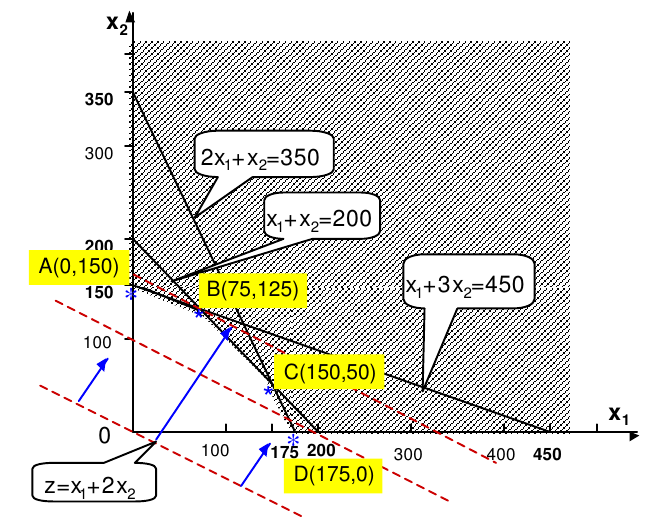
Le Simplex
Méthode graphique Le problème: Entreprise fabrique des voitures de type A et B. Il y a trois ateliers: – Atelier 1 fabrique les moteurs. – Atelier 2 fabrique les carrosseries. – Atelier 3 effectue les assemblages. Les capacités de travail des trois ateliers sont: – 450 heures par mois pour l’atelier 1. – 350 heures…
Écrit par
-
Problème d’affectation
Affecter 4 personnes à 4 taches comment faire? Soit 4 personnes A, B,C,D et 4 taches a,b,c,d La méthode hongroise tableau représentant les coefficients de préférence des différentes personnes: A B C D E a 9 6 7 3 4 b 2 1 9 1 8 c 4 3 2 2 7 d 9 1…
Écrit par
-
Methode de Balas-Hammer
Méthode On calcule pour chaque rangée, ligne ou colonne, la différence entre le coût le plus petit avec celui qui lui est immédiatement supérieur. Affecter à la relation de coût le plus petit correspondant à la rangée présentant la différence maximale la quantité la plus élevée possible. Ce qui sature une ligne ou une colonne.…
Écrit par
-
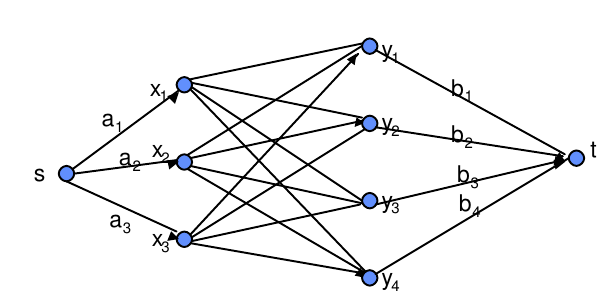
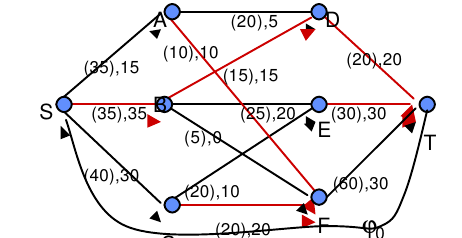
Les flots
Calcul du flot maximum dans un graph reliant le puits (t) à la source(s). Il faut respecter la loi de kirshoff: l’ensemble flux entrant sur un nœud=l’ensemble des flux sortant du même nœud Algorithme de Ford -Fulkerson Recherche du flot complet On fait passer un flot au juger Améliorer le flot jusqu’à ce qu’on ait…
Écrit par
-
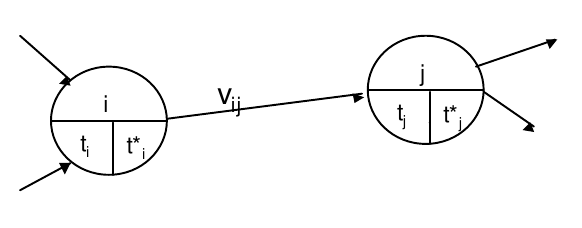
PERT
METHODE MPM (méthode des potentiels Metra- 1958) Graphe potentiel tâche Graphe orienté sans circuit de valeur positive: sommets: tâches arcs: contraintes d’antériorité entre deux tâches valués avec la durée de la tâche La recherche du plus long chemin sur le graphe valué par les durées des tâches détermine la date au plus tôt de réalisation…
Écrit par
-
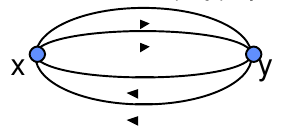
Graph Particulier
Graph Symétrique – Si pour toute paire de sommets (x,y) $\in$ X il existe autant d’arcs de la forme (x,y) que de la forme (y,x) – Cas du 1-Graphe G=(X,U), il est symétrique ssi : (x,y) $\in$ U (y,x) $\in$ U Graph Anti-Symétrique – Si pour toute paire de sommets (x,y) C $\in$ X il…
Écrit par
-
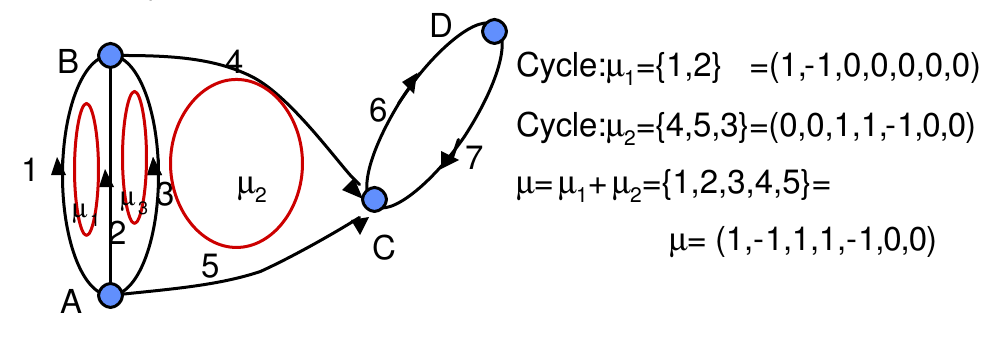
Nombre cyclomatique
Définition : Dans un graphe G=(X,U) un cycle est une séquence d ’arcs :m=(u1,u2,u3,…,uq) telle que : Tout arc uk (1
Écrit par
-
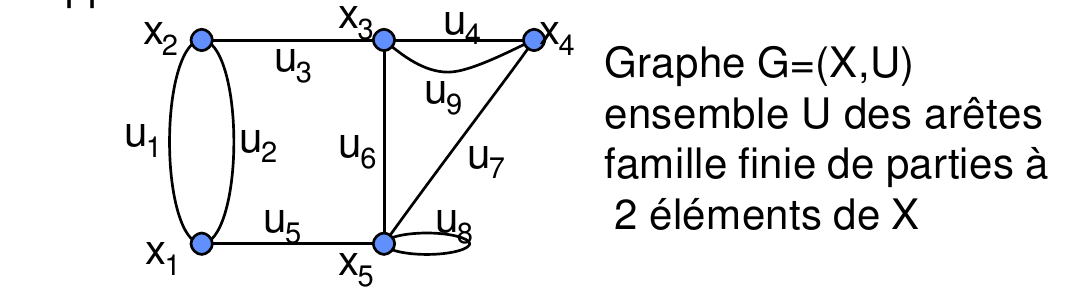
Généralités sur les graphes
La théorie des graphes : Un graphe est composé de sommets (on parle aussi de noeuds) et d’arcs qui relient les sommets entre eux. La forme n’a pas d’importance mais en général on le lit de gauche à droite, parfois de haut en bas, car ce sont des sens naturels. On appelle un graphe G(X,U)…
Écrit par
-
Calcul matriciel
Rappels sur le calcul matriciel et booléen Addition de matrices [0150]+ [1203] = [1353] [1210] [0024] [1234] Multiplication de matrices Calcul booléen le + correspond au « OU » 0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 1 pour les produits : le * correspond au…
Écrit par