Méthode graphique
Le problème:
Entreprise fabrique des voitures de type A et B. Il y a trois ateliers:
– Atelier 1 fabrique les moteurs.
– Atelier 2 fabrique les carrosseries.
– Atelier 3 effectue les assemblages.
Les capacités de travail des trois ateliers sont:
– 450 heures par mois pour l’atelier 1.
– 350 heures par mois pour l’atelier 2.
– 200 heures par mois pour l’atelier 3.
Bénéfices unitaires dégagés par l’entreprise sont::
– 4000 francs pour les voitures de type A.
– 8000 francs pour les voitures de type B.
Le tableau ci-après indique les temps unitaires de chaque opération pour chaque type de voitures
Utilisation des ressources pour fabriquer les voitures
| Voiture type A | Voiture type B | |
| Atelier Moteur | 1 | 3 |
| Atelier Carrosserie | 2 | 1 |
| Atelier assemblages | 1 | 1 |
Question: Optimiser la production de façon à obtenir le bénéfice le
plus élevé possible
Mise en équation
Soit:
– x1 production mensuelle de voitures de type A.
– x2 production mensuelle de voitures de type B.
Programme linéaire décrivant le problème:
– les contraintes de disponibilité d’heures de travail de chaque atelier (contraintes explicites)
– la fonction économique z que l’on veut maximiser.
Exemple de l’atelier 1
- il faut 1h par voiture A et 3h par voiture B : 1*x1+3*x2
- maximum 450h
ce qui donne :
Pour maximiser le bénéfice
$Max(z)=4000x_1+8000x_2$
Principe
problème peut être étudié dans R2:
2 variables x1, x2
Point M du plan : production qcq réalisable ou non.
Réalisable si : intérieur au polygone des contraintes
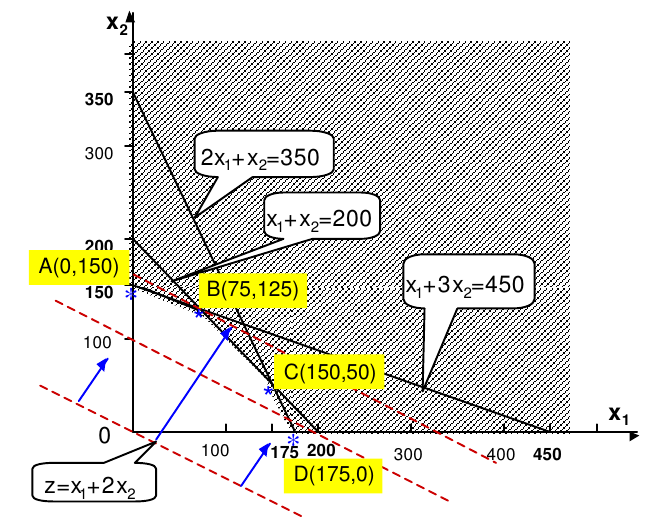
sur ce graph:
– x1 en abscisse
– x2 en ordonnée
On trace les équations:
2×1+x2<350, cette équation est modifié en remplaçant le signe < par =. Il suffira de prendre toutes les valeurs en dessous de la droite
Pour tracer on met x1=0 et on calcul x2 et inversement. Cela nous donne 2 points qui suffit pour tracer une droite.
On raie les points au dessus de cette droite car ils ne satisfont pas ma première contrainte. Pour rayer les points, on hachure
on fait pareil pour les trois inéquations, donc pour les trois contraintes
maintenant, ce qui reste en non hachuré, ce sont tous les points solutions
cet ensemble de points représente une figure géométrique qui est un polyedre ici 0, A, B, C, D
Tous les points dans la zone blanche (y compris sur les traits) sont solutions
Calcul du bénef max:
– le bénéfice vaut z = 4000 x1 + 8000 x2 on divise par 4000 pour simplifier.
– le bénéfice vaut z (z’) = x1 + 2 x2
Cette droite passe par 0, en effet si je produit 0 voiture A et 0 voiture B, le bénéfice sera de 0,
on fixe 2 variables x1=0, x2=0 => calcul de z qui est égale à 0.
Pour tracer cette droite, il nous faut un autre point avec z toujours=0.
Exemple : x1=200
0=200+2×2, => x2=-100
Ensuite, on cherche une droite parallèle a cette droite initiale qui soit la plus haute possible. Il suffit de monter pour être parallèle à cette droite et cela tant que vous restez dans le polyedre et le dernier point est le point B(75;125) qui est la meilleur solution.
On produira 75 voiture A et 125 voiture B, le bénéfice est de
Méthode des tableaux
Étape 1
On reprend les équations de départ:
Étape 2
Pour ne pas avoir d’inéquation on pose: – $x_1+3x_2+x_3=450$ avec $x_3$>0 c’est identique à $x_1+3x_2 \le 450$ – x3 représente ici le temps disponible pour l’atelier moteur
Ce qui nous donne pour toutes les équations:
$x_1+3x_2 +x_3= 450$
$2x_1 + x_2 +x_4=350$
$x_1 + x_2 +x_5= 200$
$Max(z)=x_1+2x_2$
Sous la forme matriciel
$\left[ \beginarrayrrrrr 1 & 3 & 1 & 0 & 0 \\ 2 & 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 1 \endarray \right] \cdot \left[ \beginarrayr x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \endarray \right] = \left[ \beginarrayr 450 \\ 350 \\ 200 \endarray \right]$
$Max (z)= \left[ \beginarrayrrrrrr 1 & 2 & 1 & 0 & 0 & 0 \endarray \right] \cdot \left[ \beginarrayr x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \endarray \right]$
Étape 2
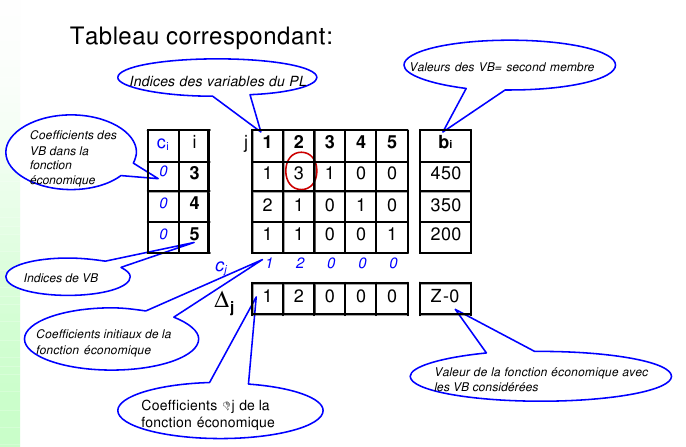
Au départ on initialise avec un bénéfice de 0 donc z=0
Déroulement de l’algorithme
On regarde la plus grande valeur dans la ligne delta j (∆j) donc tout en bas. Ici c’est 2.
La colonne 2 vas entrer en base.
Chercher la ligne du pivot
Pour cela, on divise chaque Bi par la valeur de la ligne pivot, ici la colonne 2 (qu’on vient de choisir)
On retient le plus petit ici 150, la ligne 1.
Le pivot est la colonne 2 ligne 1.
Pour la suite on écrit i=2 à gauche, là ou on avait i=3.
La colonne 2 sort, donc elle passe en ligne à la place de la ligne que l’on traite.
Pour la ligne du pivot, on divise la ligne par la valeur du pivot:
Nouvelle valeur= ancienne valeur / Valeur du pivot
La ligne du pivot: 1,3,1,0,0,0,450
Le pivot 3 (colonne 2)
Ce qui donne 1/3;1;1/3;0;0;150
| L1 (origine) | 1 | 3 | 1 | 0 | 0 | 450 |
| L1 (calcul) | 1/3 | 3/3 | 1/3 | 0/3 | 0/3 | 450/3 |
| L1 (résultat) | 1/3 | 1 | 1/3 | 0 | 0 | 150 |
Pour les lignes suivantes:
nouvelle valeur = ancienne valeur moins 1/3 de la ligne 1
nouvelle valeur = ancienne valeur – α * par l’ancienne valeur de la ligne pivot
Le coefficient alpha se calcule sur la colonne du pivot :
α = ancienne ligne / ancienne ligne du pivot
La deuxième ligne:
α = 1/3
| L2 (origine) | 2 | 1 | 0 | 1 | 0 | 350 |
| L2 (calcul) | 2 -1/3*1 | 1 -1/3*3 | 0 – 1/3*1 | 1 -1/3*0 | 0 -1/3*0 | 350-1/3*450 |
| L2 (résultat) | 5/3 | 0 | -1/3 | 1 | 0 | 200 |
La troisième ligne
α = 1/3
| L3 (origine) | 1 | 1 | 0 | 0 | 1 | 200 |
| L3 (calcul) | 1 –1* (1/3) | 1 – 1*1 | 0 – 1*(1/3) | 0 – 1/3*0 | 1 – 1/3*0 | 200 – 1/3*450 |
| L3 (résultat) | 2/3 | 0 | -1/3 | 0 | 1 | 50 |
Les deltat (r)
α = 2/3
| rj (origine) | 1 | 2 | 0 | 0 | 0 | 0 |
| rj (calcul) | 1 – 2/3*1 | 2 – 2/3*0 | 0 – (2/3)*1 | 0 – 2/3*0 | 0 – 2/3*1 | 0 – 2/3*450 |
| rj (résultat) | 1/3 | 0 | -2/3 | 0 | 0 | 300 |
ce qui nous donne:
| j=1 | j=2 | j=3 | j=4 | j=5 | Bi | ||
| i=2 | 1/3 | 1 | 1/3 | 0 | 0 | 150 | |
| i=4 | 5/3 | 0 | -1/3 | 1 | 0 | 200 | |
| i=5 | 2/3 | 0 | -1/3 | 0 | 1 | 50 | |
| $\Delta$j | 1/3 | 0 | -2/3 | 0 | 0 | -300 | |
| z=-300 |
On recommence l’algorithme
La plus grande valeur dans les delta est la colonne 1 de valeur 1/3.
$150 \over 1 \over 3$ $=150$, $200 \over 5 \over 3$ $= 120$, $200 \over 2 \over 3$ $= 75$
Le plus petit 75
Notre pivot est la ligne 3 colonne 1: (2/3).
Pour la suite on écrit i=1 à gauche, là ou on avait i=5
La ligne Pivot (Ligne 3)
On divise la ligne 3 par le pivot soit 2/3:
Ligne de pivot : 2/3;0;-1/3;0;1;50
Le pivot 2/3
ce qui donne: 1; 0; -0.5; 0; 1.5; 75
| L3 (origine) | 2/3 | 0 | -1/3 | 0 | 1 | 50 |
| L3 (calcul) | (2/3)/(2/3) | 0/(2/3) | (-1/3)/(2/3) | 0/(2/3) | 1/(2/3) | 50/(2/3) |
| L3 (résultat) | 1 | 0 | -1/2 | 0 | 3/2 | 75 |
Calcul de la ligne 1
α = (1/3)/(2/3)=1/2
| L1 (origine) | 1/3 | 1 | 1/3 | 0 | 0 | 150 |
| L1 (calcul) | 1/3-(1/2)*(2/3) | 1-(1/2)*0 | 1/3-(1/2)*0 | 0-(1/2)*0 | 0-(1/2)*0 | 150-(1/2)*50 |
| L1 (résultat) | 0 | 1 | 1/2 | 0 | -1/2 | 125 |
Calcul de la ligne 2
α = (5/3)/(2/3)=5/2
| L1 (origine) | 5/3 | 0 | -1/3 | 1 | 0 | 200 |
| L1 (calcul) | 5/3-(5/3)*(2/3) | 0-(5/2)*0 | -1/3-(5/2)*(1/3) | 1-(5/2)*0 | 0-(5/2)*1 | 200-(5/2)*50 |
| L1 (résultat) | 0 | 0 | 1/2 | 1 | -5/2 | 75 |
| $\Delta$j (origine) | 1/3 | 0 | -2/3 | 0 | 0 | -300 |
| $\Delta$j (calcul) | 1/3-(1/3)*(2/3) | 0-(1/2)*0 | -2/3-(1/2)*(-1/3) | 0-(1/2)*1 | 0-(1/2)*1 | -300-(1/2)*50 |
| $\Delta$j (résultat) | 0 | 0 | -1/2 | 0 | -1/2 | -325 |
Tous les deltas sont négatifs ou nuls, donc l’algorithme s’arrête.
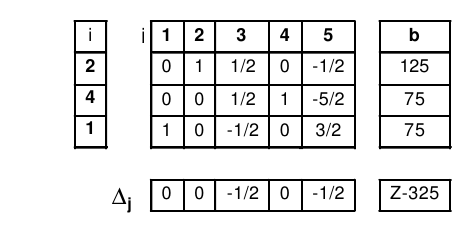
x1=75, x2=125,x3=0, x4=75, x5=0, z=325
Les ateliers 1 et 2 sont utilisés au maximum, l’atelier 3 dispose d’une réserve de 75
On peut finir en reprenant les équations de départ et surtout le bénéfice max:
$x_1=75` x_2=125$
$75+3 \cdot 125 = 450$ (atelier 1, au max)
$2 \cdot 75 + 125 = 275$ (atelier 2, pas au max)
$75 + 125 = 200$ (atelier 3, au max)
$1300000 = 4000 \cdot 75 + 8000 \cdot 125$