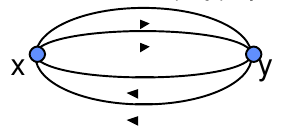
– Cas du 1-Graphe G=(X,U), il est symétrique ssi : (x,y) $\in$ U (y,x) $\in$ U
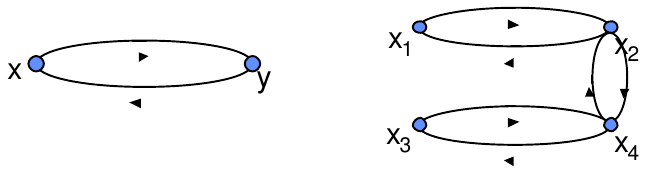
Graph Anti-Symétrique – Si pour toute paire de sommets (x,y) C $\in$ X il n’existe pas autant d’arcs de la forme (x,y) que de la forme (y,x) Le graphe G est dit anti-symétrique – Cas du 1-graphe G=(X,U) il est anti-symétrique ssi :
(x,y) $\in$ U $\Rightarrow $ (y,x) $\in$ U
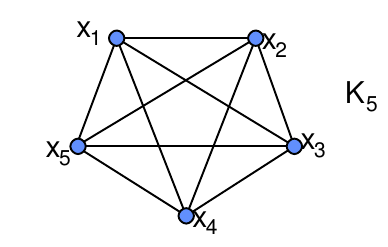
Graph complet
– Un graghe G est complet si:
$m_G$ (x,y) = $m^+_G$(x,y)+$m^–_G$(x,y) $\geq$ 1 pour tout x,y $\in$ X avec x $\neq$ y
– Si G est un 1-graphe il est complet ssi : (x,y) $\notin$ U $\Rightarrow$ (y,x) $\in$ U
Les arbres :
DEFINITION:
Graphe connexe sans cycle
Soit n sommets(n>=2) on obtient un arbre en joignant les n sommets sans former de cycle. Cet arbre a (n-1) arêtes
Preuve :
- vrai si n=2: arbre à une arête
- Supposons cela vrai pour (n = k-1) arêtes:
- arbre obtenu en connectant (k-1) sommets sans jamais former de cycle, (k-2) arêtes
- Ajoutons un keme sommet pour rendre le graphe connexe il suffit de relier le nouveau sommet à l’un des (k-1) sommets par une arête
- (k-2)+1=k-1 arêtes
- (k-1)+1=k sommets
Un arbre est un graphe connexe sans circuit, donc en un seul morceau et sans « boucle »
THEOREME:
Soit H =(X,U) un graphe d ’ordre card(X)=n>=2
Les propriété suivantes caractérisent un arbre :
- H est connexe et sans cycle
- H est sans cycle et admet (n-1) arêtes
- H est connexe et admet (n-1) arêtes
- H est sans cycle et en ajoutant une arête on crée un cycle et un seul
- H est connexe et si on supprime une arête qcq, il n ’est plus connexe.
- Tout couple de sommets est relié par une chaîne et une seule.
Arbre recouvrant minimal
Algorithme de Kruskal
- Faire le liste des arêtes par valuation croissante.
- S ’il existe des valeurs identiques ajouter une valeur ε à la première, 2ε à la suivante. n ε à la $n^eme$. ε doit satisfaire la condition suivante : $n \epsilon + v_i \leq v_i +n$
- Choisir l’arête de valeur minimale, puis successivement, au fur et mesure de la construction de l’arbre, l’arête de valeur immédiatement supérieure dans la liste mais sans former de cycle avec les arêtes déjà retenues.
- Arrêt lorsque tous les sommets sont connectés nombre d’arêtes=n-1
La complexité est en O(m log m).
donc plus m grandit, plus les temps de réponse seront énormes
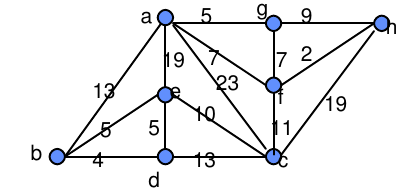
| ab=13 | fa=7 |
| be=5 | fc=11 |
| bd=4 | ga=5 |
| ea=19 | gf=7 |
| ec=10 | hf=2 |
| ed=5 | hg=9 |
| cd=13 | hc=19 |
| ca=23 |
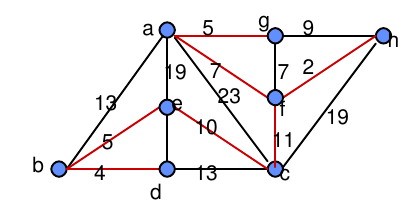
| hf=2 | ec=10 |
| bd=4 | fc=11 |
| be=5 | ab=13 |
| ed=5,(1) | cd=13,(1) |
| ga=5,(2) | |
| gf=7 | hc=19 |
| fa=7,(1) | ea=19,(1) |
| hg=9 | ca=23 |
Algorithme de Sollin
je prends le premier A
Quel est l’arrête qui va vers A qui coute le moins cher ?
F=3
mon paquet devient $\$A, F$\$
Le point suivant c’est B, le moins cher est $\$B,E$\$ un $2^eme$ paquet
Le point suivant est C, le moins cher est $\$C,B$\$, le $2^eme$ paquet devient $\$C,B,E$\$
Le point suivant D, le moins cher est $\$D,G$\$, le $3^eme$ paquet $\$D,G$\$
On recommence avec les 3 paquets $\$A,F$\$, $\$C,B,E$\$ et $\$D,G$\$
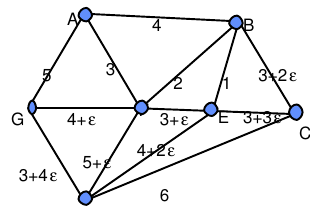
$c_1$=$\$A$\$;$c_2$=$\$B$\$; $c_3$=$\$C$\$; $c_4$=$\$D$\$; $c_5$=$\$E$\$; $c_6$=$\$F$\$; $c_7$=$\$G$\$;
$c_1$ non marqué, $v_1j$=min($c_1$,j)=[A,F]marquer $c_1$ et $c_6$
$c_2$ non marqué, $v_2j$=min($c_2$,j)=[B,E]marquer $c_2$ et $c_5$
$c_3$ non marqué, $v_3j$=min($c_3$,j)=[C,B]marquer $c_3$et $c_5$
$c_4$ non marqué, $v_4j$=min($c_4$,j)=[D,G]marquer $c_4$et $c_7$
Tous les $c_i$ sont marqués,
$U_1$= [A,F], [B,E], [C,B], [D,G] —> étape 2
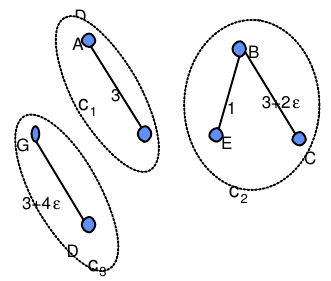
Sous-arbres :
$c_1$=$\$A,F$\$, $c_2$=$\$B,C,E$\$, $c_3$=$\$G,D$\$,
$c_1$ non marqué, $v_1,j$ =min ($c_3$,j)=[B,F]marquer $c_1$ et $c_2$
$c_3$ non marqué, $v_1,j$ =min ($c_3$,j)=[G,F]marquer $c_3$ et $c_1$
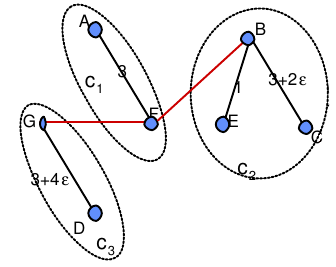
Sous-arbres :
$c_1$=$\$A,F$\$, $c_2$=$\$B,C,E$\$, $c_3$=$\$G,D$\$,
$c_1$ non marqué, $v_1,j$ =min ($c_1$,j)=[B,F]marquer $c_1$ et $c_2$
$c_3$ non marqué, $v_1,j$ =min ($c_3$,j)=[G,F]marquer $c_3$ et $c_1$
Tous les ci sont marqués
$U_2$=$\$U1, [B,F] ,[G,F]$\$
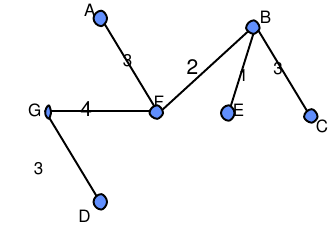
On obtient l ’arbre recouvrant A qui est minimal $\lambda$(A)=16